| Pierre CRESPIN | Pourquoi ? Pourquoi ? Pourquoi ? | Pavage du plan par le pentagone Penta15 |
Pourquoi ? Pourquoi a-t-il fallu autant de temps pour découvrir ce dernier pentagone pavant le plan, pentagone possédant des propriétés que j’estime assez particulières et remarquables. Et donne au pavage réalisé des propriétés non moins intéressantes.
Pourquoi ? Pourquoi
ce pavage est-il unique ? (à un déplacement ou anti-déplacement près )
Pourquoi ? Pourquoi
n’a-t-on pas trouvé ce pavage à partir d’une tentative de pavage du plan avec
un mix d’hexagones et de carrés dont les cotés auraient même longueur. Mais
peut-être cela a-t-il été le cas, ou y a-t-il eu des tentatives de ce type ?
Tout en étant de plus en plus persuadé que les bonnes propriétés de ce pentagone (que je continue à appeler Penta15 pour le distinguer des 14 précédents) sont une bonne raison de ce choix, je ne suis toujours pas convaincu de la validité de mes arguments. Et je crois qu’il est nécessaire de faire un appel à la cantonade. Je joindrai ici les figures Cabri qui me paraissent les plus convainquantes.
lire la suite (Quelques pistes, remarques, et compléments en vrac)
En attendant , rappels et compléments pour les calculs de longueurs et d’aires
[AE] a pour longueur 2, le coté [BC] a une mesure irrationnelle (rac(2)*(1+rac(3))/2 #1,93…
proche de 2 !
Les deux grands cotés de Penta15 sont donc très proches. Et les autres cotés ont pour mesure 1.
Pour certaines figures on nommera les côtés 0 (BC, irrationnel), puis, dans l’ordre 1, 2, 3, 4 ayant pour mesure 1, sauf 2 ayant pour mesure 2 !!
et ce pour les deux pavés (droit ou gauche): 0 pour le côté irrationnel, 2 pour le côté de mesure 2, les autres côtés 1, 3, 4 ayant pour mesure 1.
On notera que AC = AC' = 1 + Aa = 1 + rac(3) est la norme du vecteur de la translation potentielle plus ou moins évidente.
A propos de la tentative de pavages avec carrés et demi-hexagones / hexagones mis en évidence par le pavage par Penta15.
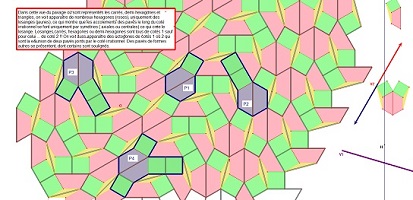
Le pavage réalisé avec des pentagones Penta15 où figurent les trois
parties constitutives montre mieux les translations et symétries .
De
plus AC =1 + rac(3) est évident sur certaines figures.
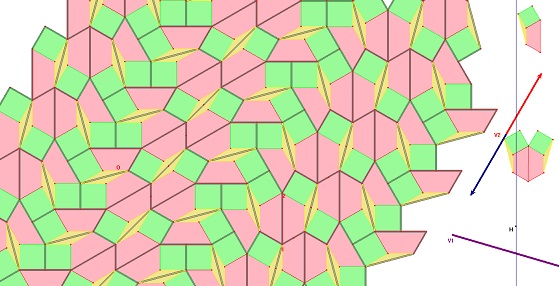
De même pour la découverte de la deuxième translation, des centres de
symétrie et des anti-déplacements laissant le pavage invariant.
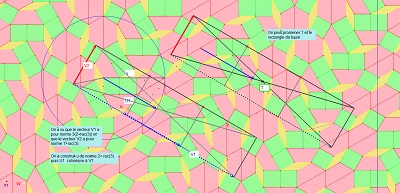
Voir une figure du rectangle de base , avec construction du vecteur dont la norme est 3(2+rac(3)), où 2+rac(3) est visualisé .
 |
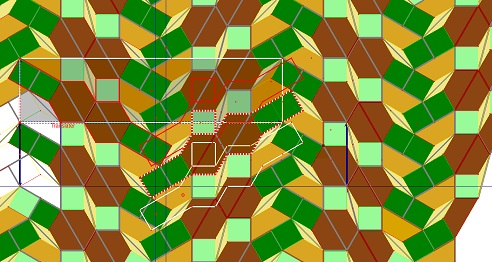 |
Le pavage par Penta15 conduit-il à ce pavage optimal? ou peut-on le rechercher avec un autre fil directeur? A suivre...
Accès à Reponses.html ou ImagesReponses.html (mieux) ou aller plus rapidement à la conclusion